| تاریخ انتشار | ۲۶ مرداد ۱۳۹۳ |
| عنوان انگلیسی | Accident Pattern Estimation and Real Time Accident Detection |
با دریافت اطلاعات مسیر حرکت خودروها به صورت برخط و تشخیص الگوی حرکتی آنها در هر بخش از خیابانها، میتوان این الگوها را با الگوهای زمان سفر که در پایگاه داده الگوهای ترافیکی نگهداری میشود، منطبق کرد. در نتیجه با ترکیب نتایج میتوان، یک وضعیت خاص ترافیکی را تشخیص داد. برای مثال اگر زمان سفر در یک بخش، به صورت ناگهانی تغییر کند، نشان از یک واقعه مانند تصادف دارد. از سوی دیگر در این پایاننامه الگوهای ترافیکی گوناگون مانند تصادف را مورد بررسی قرار میدهیم. به این ترتیب با تطبیق این الگوها با هم، میتوانیم وقایعی مانند تصادف را به صورت برخط تشخیص دهیم.
در ابتدا باید تشخیص وقوع یک واقعه خاص در یک نقطه تفسیر شود. در واقع ما به راحتی نمیتوانیم وقوع یک تصادف در یک نقطه خاص را بیان کنیم، بلکه تنها میتوان صحبت از احتمال وقوع یک تصادف یا حادثه در یک نقطه خاص کرد. ساختار ساده شدهی یک تصادف به صورت کلی در شکل ۸ نشان داده شده است.

با بروز یک تصادف گرفتگی بعد از آن شروع شده و طول این گرفتگی با گذشت زمان بیشتر میشود. با نگاه به مدل موجود در معماری مبتنی بر مسیر، اگر یک گرفتگی در یک قطعه خیابان ایجاد شود، این گرفتگی به مرور به قطعههای منتهی به قطعه مورد نظر منتقل شده و این روند ادامه پیدا خواهد کرد. جریان ورود خودروها به قطعه مورد نظر بیش از جریان خروجی شده و نسبت ورود به خروج، رشد طول صف ایجاد شده را مشخص میکند. این رشد از ابتدای قطعه و با ایجاد شاخههای مختلف دیگر به راحتی قابل تشخیص نمیباشد. ولی به طور کلی خود مسئلهای است که در پایان این فصل کمی به آن پرداخته خواهد شد. در نهایت برای سادهسازی مسئله فرض میکنیم در طول زمانهای مشخص قطعه خیابانهای منتهی به مرور مسدود میشوند و تاثیر تصادف در خیابانهای یک سطح بعد هم دیده خواهد شد. در واقع اگر فاصله هر قطعه تا قطعه تصادف را در نظر بگیریم، فرض میکنیم بعد از زمان T (عددی بین ۲ تا ۵ دقیقه) تاثیر تصادف در قطعات با فاصله ۱ دیده شده و بعد از زمان ۲T تاثیر تصادف در قطعات با فاصله ۲ دیده میشود و این روند در طول زمان ادامه پیدا میکند. همچنین فرض میکنیم با گذشت زمان حداکثری T_a، حتی در صورتی که نمونهای از محل مورد نظر عبور نکند، مشکل تصادف مرتفع خواهد شد.
از نگاه مشاهدهگر، با دیدن یک گرفتگی در یک قطعه، پی میبریم که در قطعه مورد نظر یا قطعات بعدی گرفتگی ایجاد شده است. در نتیجه به صورت احتمالی، احتمال بروز تصادف در قطعه خیابانهای بعد از قطعه مشاهده شده، بررسی میشود.
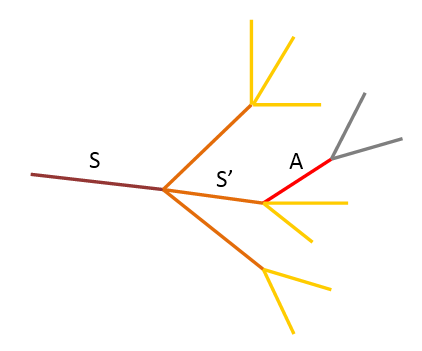
طبق شکل ۲، فرض میکنیم مشاهده در قطعه S و تصادف در قطعه A اتفاق افتاده باشد. فرض میکنیم احتمال تصادف در قطعه مشاهده شده µ و با هر یک واحد فاصله قطعات از محل مشاهده، احتمال بروز تصادف در α ضرب شود و احتمال وقوع تصادف تا زمانی جلو میرود که از حد T_a نگذرد. به این ترتیب قطعات با فاصله حداکثر k برای احتمال تصادف در نظر گرفته میشوند. برای مثال در شکل ۹، احتمال وقوع تصادف (مقدار µ) با فرض مشخص کردن α به شکل زیر محاسبه میشود (فرض میکنیم احتمال تصادف تا ۲ قطعه خیابان بعد از محل مشاهده ممکن میباشد، در واقع k=2):
![]()
با ادامه حرکت مشاهدهگر، اگر مشاهدهگر از یکی از قطعههای غیر از S’ حرکت کند، تنها احتمال تصادف معطوف به دو مسیر دیگر شده و بار دیگر قابل اندازهگیری میباشد. همچنین با این اتفاق احتمال وجود تصادف در قطعه S کماکان باقی میماند. در نتیجه که در مثال شکل ۸ برابر میشود با:
![]()
همچنین اگر مشاهدهگر از قطعه S’ حرکت کند، این احتمال معطوف به قطعه S’ و قطعات بعد از آن میشود با این تفاوت که حد تخمین ۱ واحد کاهش پیدا کرده و احتمال تصادف تا k-1 رده محاسبه میشود. به این ترتیب برای مثال شکل ۸ خواهیم داشت:
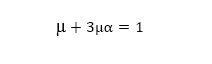
حال فرض میکنیم مشاهداتی از نمونههای مختلف در یک منطقه بدست بیاید. در این صورت باید روشی برای برهمنهی احتمالات داشته باشیم. هر یک از مشاهدات ما فضای احتمالاتی برای تصادف بوجود میآورد. حال فرض کنید فضای احتمالاتی دو مشاهده اشتراک داشته باشد. وجود دو مشاهده گرفتگی میتواند نشان از دو تصادف مختلف داشته باشد، ولی بدلیل آنکه دو مشاهده در نزدیکی یکدیگر اتفاق افتاده و دارای اشتراک میباشند، با کمی اغماض میتوان فرض کرد که تصادف در محل اشتراک دو مشاهده اتفاق افتاده است. به همین دلیل فضای احتمال بالا را برای فضای اشتراک دو مشاهده ایجاد میکنیم و ملاک ما برای در نظر فاصله، کمینه فاصله هر قطعه به هر یک از قطعات مشاهده میباشد.
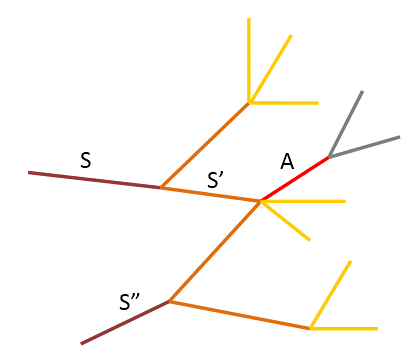
با در نظر گرفتن مثال شکل ۹، اگر فرض کنیم مشاهدات در دو قطعه S و S” اتفاق افتاده باشد، داریم:
![]()
به همین روش میتوان برای مشاهدات بیشتر موضعی عمل کرد.
در هر صورت، ممکن است مشاهدهگری در زمان مناسب به محل تصادف نرسیده و در نتیجه تصادف کشف نشود. در این صورت تنها احتمال وقوع تصادف در قطعات مختلف برای ما باقی خواهد ماند. در این حالت تاثیر ایجاد صف در پشت نقطه تصادف در احتمال وقوع تصادف در قطعه مورد نظر ضرب میشود و این تاثیر برای خیابانهای مختلف محاسبه میشود.
فرض میکنیم با احتمال p در قطعه A تصادف شده باشد. تمام قطعاتی که با محدودیت T_a مسیری به قطعه A دارند را در نظر بگیرید. فرض میکنیم زمان سفر در قطعه A از زمان تصادف تا رسیدن سیستم به حالت عادی را داشته باشیم (TT_A(t)). با هر واحد دور شدن قطعات از قطعه A، این تابع برای قطعات بعدی با در نظر گرفتن ضریب محاسبه میشود. در واقع اگر قطعهای با فاصله ۲ به قطعهA برسد، ضریب تاثیر تابع زمان سفر در هنگام تصادف برای این قطعه خواهد بود. بدست آوردن تاثیر تصادف در زمان سفر و جریان ترافیک مسئلهی مناسبی برای تحقیق میباشد که در {؟} و {؟} هم به آن پرداخته شده است.
تشخص روان شدن ترافیک قطعههایی که در یک تصادف درگیر بودهاند، خود مسئله پیچیدهای میباشد. در واقع سرعت حل مشکل تصادف در مواقع و حالتهای مختلف متفاوت است. در نتیجه تابع زمان سفر در زمان تصادف یک حالت پیشفرض داشته و با حل سریع تصادف دچار کشیدگی در محور زمان میشود. حال اگر مشاهدهای از یک قطعه انجام پذیرد که وضعیت زمان سفر روانتر از حالت پیشفرض زمان سفر به هنگام تصادف با توجه به ضرایب تاثیر در قطعه مورد نظر باشد (در صورتی که ضرایب تاثیر مناسب انتخاب شده باشند)، میتوان فرض کرد تصادف رخ داده زودتر از زمان پیشفرض حل شده است. در این صورت با توجه به مشاهده انجام شده، نقطه مناسب بر روی تابع زمان سفر به هنگام تصادف برای قطعه مشاهده شده محاسبه شده و قطعههای منطقه تصادف به صورت مشابه دچار کشیدگی در طول زمان میشوند و در نتیجه وضعیت ترافیک و زمان سفر در همه قطعات بروزرسانی میشود. این حالت ممکن است ما را به نقطهای برساند که بتوانیم حل گرفتگی ایجاد شده بر اثر تصادف و رسیدن به شرایط پایدار را نتیجهگیری کنیم.
روشهای کلی گفته شده در این فصل برای ارائه راه حل کلی در این روش و معماری بوده است تا بتوانیم گرفتگیهای حاصل از تصادف را تشخیص دهیم. به دلیل اینکه تعداد تصادفاتی که ممکن است در یک لحظه در شهر اتفاق بیفتد کم میباشد، میتوان روشها و تحلیلهای پیچیدهتری را برای تشخیص تصادف و تخمین زمان سفر به هنگام تصادف به کار ببریم که نیاز به تحقیق بیشتری دارد. همچنین تخمین زمان سفر به هنگام تصادف خود مقولهای است که در این فصل به آن نخواهیم پرداخت. مطالعات و شبیهسازیهای زیادی در این باره صورت گرفته است که به صورت مناسبی قابل انطباق برای استفاده در این معماری میباشند که به یکی از این روشها بر مبنای ایده Kalman Filter در فصل {۲٫۳٫۶} اشاره شد.
«استفاده از مطالب این وبلاگ با ذکر لینک و منبع، بلامانع است»
